Sample Machine Problem: Searching
Overview
The goal for this assignment is to get more comfortable with the search functions explored in class, and to adapt them to the problem of searching a graph.
You will be writing a program that enables the user to search for a route between any two airports, given a maximum "hop distance" --- i.e., the maximum distance between any two airports on the route. A route should not contain a given airport more than once, and in addition may not always exist for a some hop distance. For airport information, we will use the open source database maintained at OpenFlights.org.
Consider the following graph, in which the vertices represent cities in the United States. The edges between the cities represent bi-directional connections, and the labels on the edges correspond to inter-city distances. Only cities with edges between them are considered neighbors, for the purposes of traversal.
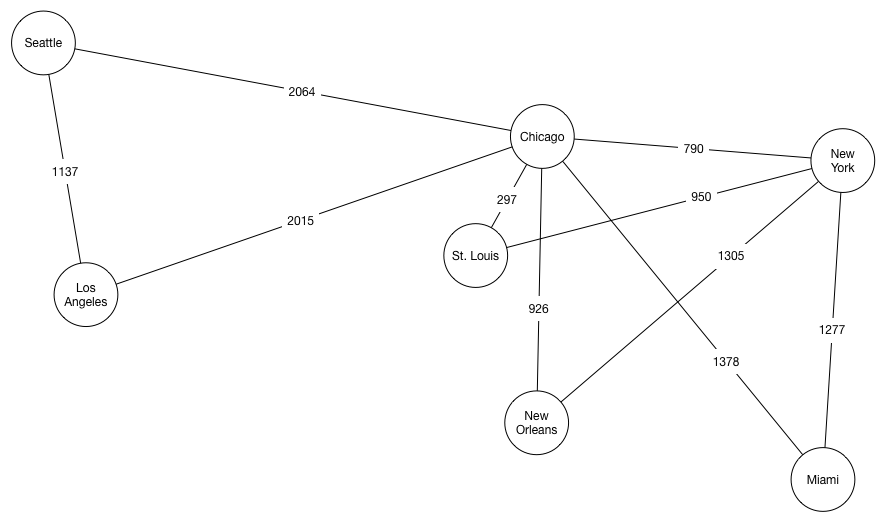
It should be clear that there are potentially multiple routes between any two vertices in the graph. From Miami to Seattle, for instance, we may choose the [Miami, Chicago, Los Angeles, Seattle] route or the [Miami, New York, Chicago, Seattle] route, among others. Routes containing cycles are also possible; e.g., [Miami, Chicago, St. Louis, New York, Chicago, Seattle]. Your solution will need to find a route without a cycle.
Each route has a corresponding distance, which is simply the sum of the edges traversed. The [Miami, Chicago, Los Angeles, Seattle] route has a total distance of 1378 + 2015 + 1137 = 4530 miles, for instance.
Building a graph from airport data
Recall that our search function will be driven by the "maximum hop distance"
between any two airports on the route --- the intuition being perhaps that we
are seeking to travel between two cities using a plane with limited range. The
cities reachable from any given city will therefore be obtained by filtering out
all cities from the dataset which are more than the maximum hop distance
away. This would form the basis of a neighbors function for our graph.
Data types and functions to compute the distance between two latitude/longitude pairs and represent routes are provided; here are some of them:
data Location = Location {
locName :: String,
latitude :: Double,
longitude :: Double
}
data Path = Path {
totalDist :: Double,
route :: [Location]
} deriving (Eq)
geoDistance :: (Double,Double) -> (Double,Double) -> Double
geoDistance (lat1,lon1) (lat2,lon2)
= 3959 * (acos (sindeg(lat1) * sindeg(lat2)
+ cosdeg(lat1) * cosdeg(lat2) * cosdeg(lon2-lon1)))
where sindeg = sin . toRadian
cosdeg = cos . toRadian
toRadian deg = pi/180.0 * deg
distanceBetween :: Location -> Location -> Double
distanceBetween (Location _ lat1 lon1)
(Location _ lat2 lon2) = geoDistance (lat1, lon1)
(lat2, lon2)
Implementation details
You are to implement the function findPath, with the following type:
findPath :: [Location] -> String -> String -> Double -> Maybe Path
The first argument is the list of locations (airports), the second and third are
the names of the origin and destination aiports, and the fourth is the maximum
hop distance. The function should return a Just Path if a route is found and
Nothing otherwise.
Testing
Below is a short list of locations suitable for testing:
lat_long_data = [ ("Bangkok", 13.76, 100.5),
("Beijing", 39.90, 116.41),
("Buenos Aires", -34.6, -58.38),
("Chicago", 41.87, -87.63),
("Dallas", 32.77, -96.79),
("Denver", 39.73, -104.99),
("Dubai", 25.20, 55.27),
("Honolulu", 21.30, -157.85),
("London", 51.50, -0.12),
("Los-Angeles", 34.05, -118.24),
("New-York", 40.71, -74.00),
("Paris", 48.85, 2.35) ]
testAirports :: [Location]
testAirports = map (\(n,lat,lon)->Location n lat lon) lat_long_data
Here are some sample routes (others are possible) discovered by a reference
implementation of findPath:
> findPath testAirports "Los-Angeles" "New-York" 1000
Just <2459.3319233721513: Los-Angeles - Denver - Chicago - New-York >
> findPath testAirports "Los-Angeles" "New-York" 500
Nothing
findPath testAirports "Chicago" "Bangkok" 4000
Just <10385.014182737235: Chicago - London - Dubai - Bangkok >
findPath testAirports "Chicago" "Bangkok" 8000
Just <8637.711070622021: Chicago - Beijing - Bangkok >
findPath testAirports "Chicago" "Bangkok" 10000
Just <8558.90431700429: Chicago - Bangkok >
findPath testAirports "Chicago" "Bangkok" 1000
Nothing