Machine Problem: Search
Overview
For this machine problem you will be modeling your own search problems and solving them using the strategies presented in class.
Specifically, you will need to select and model a search problem and devise a cost function and admissible heuristic to solve it using A* search, and a separate adversarial search problem to solve using minimax.
The hard (and fun!) part of this assignment comes down to modeling the problems you select. Problems that don't have intuitive "steps" or "moves" that help us traverse the search space can -- with some creative thinking -- be reformulated to fit our search functions. We give some examples of problems and approaches to modeling them below. In the end, though, the choice is up to you!
Starter code repository
Claim your repository via the invitation link on the class homepage and git clone your starter code.
Next, before continuing, remember to sign the honor pledge in the "package.yaml" file so we know who your submission belongs to.
Part 1: Modeling and solving a problem with A* search
Your code for this portion should go into the file "src/MP5a.hs", into which we've already copied the search functions from the lecture notes for you.
1. Pathfinding
Given a set of locations and the lengths of paths that connect them, find the shortest route between two locations. There are many variations/refinements of this problem:
-
Instead of enumerating all inter-node paths, we could enforce a maximum single-hop distance (this might be appropriate if we were modeling air travel -- all locations would be airports and a plane would be limited by range).
-
Each location en route could add additional, variable delays to the trip (large metro areas along a route can be congested).
-
Instead of pre-established paths, we could be traversing an open space with obstacles. This would require "collision testing" to determine if moving in certain directions would be hindered by obstacles. This type of pathfinding is performed in countless games/simulations featuring autonomous agents (e.g., roaming AI-driven enemies). The illustration below shows four possible routes to a goal through a space populated with obstacles.
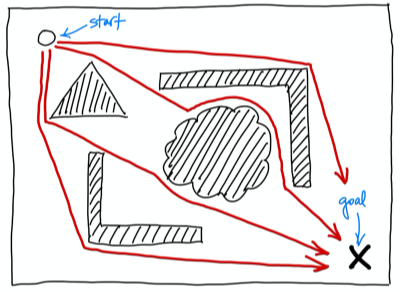
This is the most straightforward problem to model. Nodes are locations, and the cost function uses road lengths, the Pythagorean theorem, or the Haversine formula to compute distances. An admissible heuristic could simply be the straight-line distance from a location under consideration to the goal.
The result of the search should be a path consisting of all the roads or locations traversed, and the total path distance.
2. Knight's tour
A knight's tour describes a sequence of moves taken by the knight piece on an empty chessboard such that it traverses every square on the board exactly once. The animation below shows a knight's tour on a 5x5 board starting at the center square.

Nodes can represent a step along the knight's tour -- i.e., one in which the knight has traversed some number of known squares. Valid moves are easy enough to discern, but what of a heuristic for choosing between available moves? One interesting heuristic is "Warnsdorff's rule", which suggests that we prioritize moves which minimize the number of possible moves from the resulting knight position.
3. Sliding puzzle
A sliding puzzle is a game that requires the player to reorganize pieces by sliding them in fixed ways in order to create a specific configuration.
To model this problem we could have each node represent a configuration of pieces, and nodes would be connected based on valid moves (horizontal or vertical "slides"). E.g., below we have a current state for an 8-puzzle with 3 possible moves:
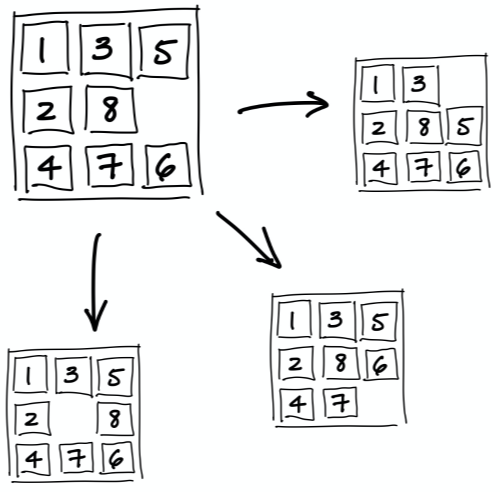
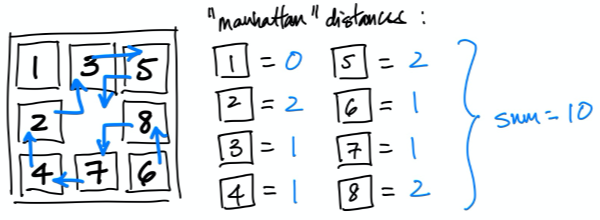
A clever heuristic we can use for estimating the minimum number of remaining moves is the sum of the Manhattan distances each piece is from its goal position. E.g., assuming the desired final configuration is for the pieces to be in ascending order, left-to-right then top-to-bottom, this heuristic would be equal to 10 for the following 8-puzzle state:
Sokoban is a fun variation on the sliding puzzle game -- though harder to model.
Part 2: Modeling and solving a problem with Minimax
For part 2 you will choose a 2-person adversarial game to model, and implement an "AI" adversary for it driven by game tree search. For simple games, it is possible you can devise deterministic algorithms for predicting the next best move or winning strategy (this is true, for instance, with simple configurations of Nim, the first game described below); however, for this assignment you must find moves based on game-tree search using minimax.
For complex games with a large search space and high branching factor, it is computationally infeasible to build the entire (or even a particularly deep) game tree. In those situations, you would prune the game tree to a fixed height and score the resulting leaves with some heuristic function(s). Coming up with useful heuristics can be challenging and fun!
Your final implementation should include a playAI IO action that allows a player to
interactively face off against your AI. The manner in which moves are specified
is up to you.
Your code for this portion should go into the file "src/MP5b.hs", into which we've already copied the minimax and related utility functions from the lecture notes for you.
1. Nim
The game of Nim involves each player removing one or more objects from separate piles (where the maximum number of objects taken each turn and the number/configuration of piles may vary); the loser of the game is the one forced to pick up the last object.
The simplest version of Nim would involve just a single pile -- a classic formulation is a pile of 21 objects -- and players alternating turns removing between 1-3 objects. This version has a simple strategy for guaranteeing a win (for which player?), but remember that your AI must pick moves using search.
2. Connect-4 / Gomoku
Connect Four and Gomoku are both variations on the "make-a-line" category of adversarial games, where pieces are placed and never moved, and the size of the game area is fixed.
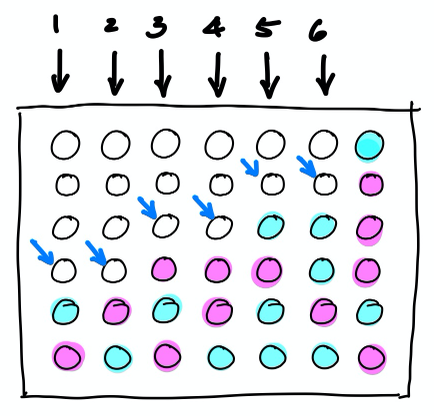
Connect Four is likely easiest to model and search, as moves are limited to just one of the (non-full) columns, and pieces will always fall to the lowest unoccupied row of a given column. In the following example, the current player may only drop a piece into one of the first 6 columns, and the piece will be deposited in the slot denoted by the blue arrow in the corresponding column. Regardless of whose turn it is, purple is headed for a win in this particular game.
3. Reversi
Reversi (or, similarly, Othello), is a board game in which players take turns placing pieces that surround and capture their opponent's pieces in orthogonal or diagonal fashion. Play continues until either no moves can be made or the board is filled, at which point the player with the most points wins. When played on a standard 8x8 board, there are approximately 1028 different possible positions in the game --- lots of room for tinkering with your scoring heuristic!
In the situation below (the solid blue and red pieces are in the standard starting positions for Othello), if it is red's turn to go there are 4 possible moves, numbered and outlined. If red chooses to make move 1, the resulting board is shown.
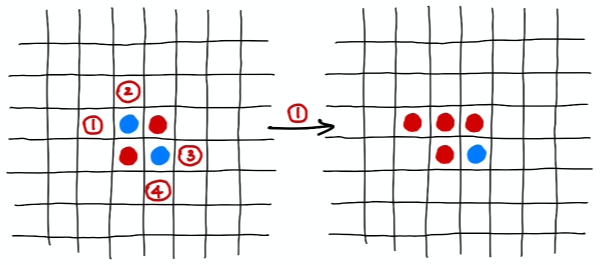
It is now blue's turn, and there are 3 moves to pick from. If blue chooses move 2, the resulting board is shown.
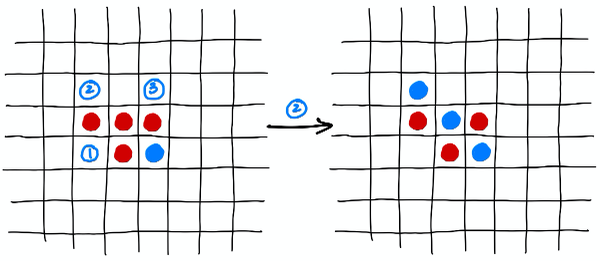
We suggest supporting boards of different sizes should you choose to model this (or a similar) game. It will make testing much easier.
On using libraries
At this point any of the modules that are part of the "base" Haskell library set are fair game. You can browse them here. We've already used plenty of functions in Data.List.
You may also find useful modules in other libraries that we've added to your repository's package configuration file, including:
- Random, which includes System.Random for generating random values
- Split, which includes Data.List.Split, a module with a bunch of functions for "splitting" lists
- Containers, which includes Data.Map, Data.Set, and Data.Tree
- Array, which includes Data.Array, for representing single/multi-dimensional arrays (with APIs for easily updating values by index)
- The Monad Transformer Library, which includes a bunch of monads that can be "stacked" together
If you have your eye on a library in the full package list that we haven't included, please ask before using it!
Testing
We encourage you to write tests for your code, but will not be enforcing it for
this machine problem. If you do write tests, please keep them separate from your
implementation source file as we did in previous machine problems. Though
unsafePerformIO is verboten in production code, it is perfectly fine for
helping you test, debug, and visualize critical parts of your implementation
during development.
Grading
Each part of this machine problem will be evaluated in three areas:
-
Did you successfully model the problem/game using data types and supporting functions? A measure of success would be to demonstrate how to load data (e.g., for your search problem or game) into values of the appropriate type, perform a "move" (e.g., add a node to the path, or take a valid turn in the game), and print out an intuitive representation of the before/after states. This last bit should ideally be enabled by custom
Showinstances. -
Did you successfully translate the task of "solving" your problem/game to searching a space of interconnected nodes for a specific "goal" node? This might require defining additional types and functions. To demonstrate this, you should be able to invoke
searchor build a game tree and pass it tominimax, using some starting state and supporting function(s), and have it return a meaningful result. -
Did you successfully solve your problem using search? For part 1, this means locating an optimal path or solution for different, non-trivial inputs. For part 2, this means creating an AI that demonstrates a viable (though not necessarily always winning) strategy for playing the game -- an interactive play function goes a long way towards demonstrating this.
Please include a very brief description of the problem/game you're choosing to model in a comment atop each of your source files, so we know what we're looking at and how best to test it!
Submission
First, make sure you correctly signed and committed the "package.yaml" file. We won't be able to easily map your repository to your name if you don't!
To submit your work, simply commit all changes and push to your GitHub repository.